Finite State Automaton
M = (Q, Σ, δ, q0, f) There is a set of states Q which M manipulates by δ over Σ and the string is accepted if it lies in f ⊂ Q, starting from q0.
q0 ∈ Q, f ⊂ Q
M always reads the entire input.
Accepting a string
Given a string, S = c0,c1…cn, M accepts S iff ∃ r0, r1, … rn+1 ∈ Q, st
- r0 = q0
- ri + 1 = δ(ri, ci)
- rn+1 ∈ f
A language is recognized by M, iff L = {s | M accepts s}.
Example
- Define a Finite State Automaton that recognizes the language L = 101, Σ = {0,1}. Look at Fig 1 for implementation.
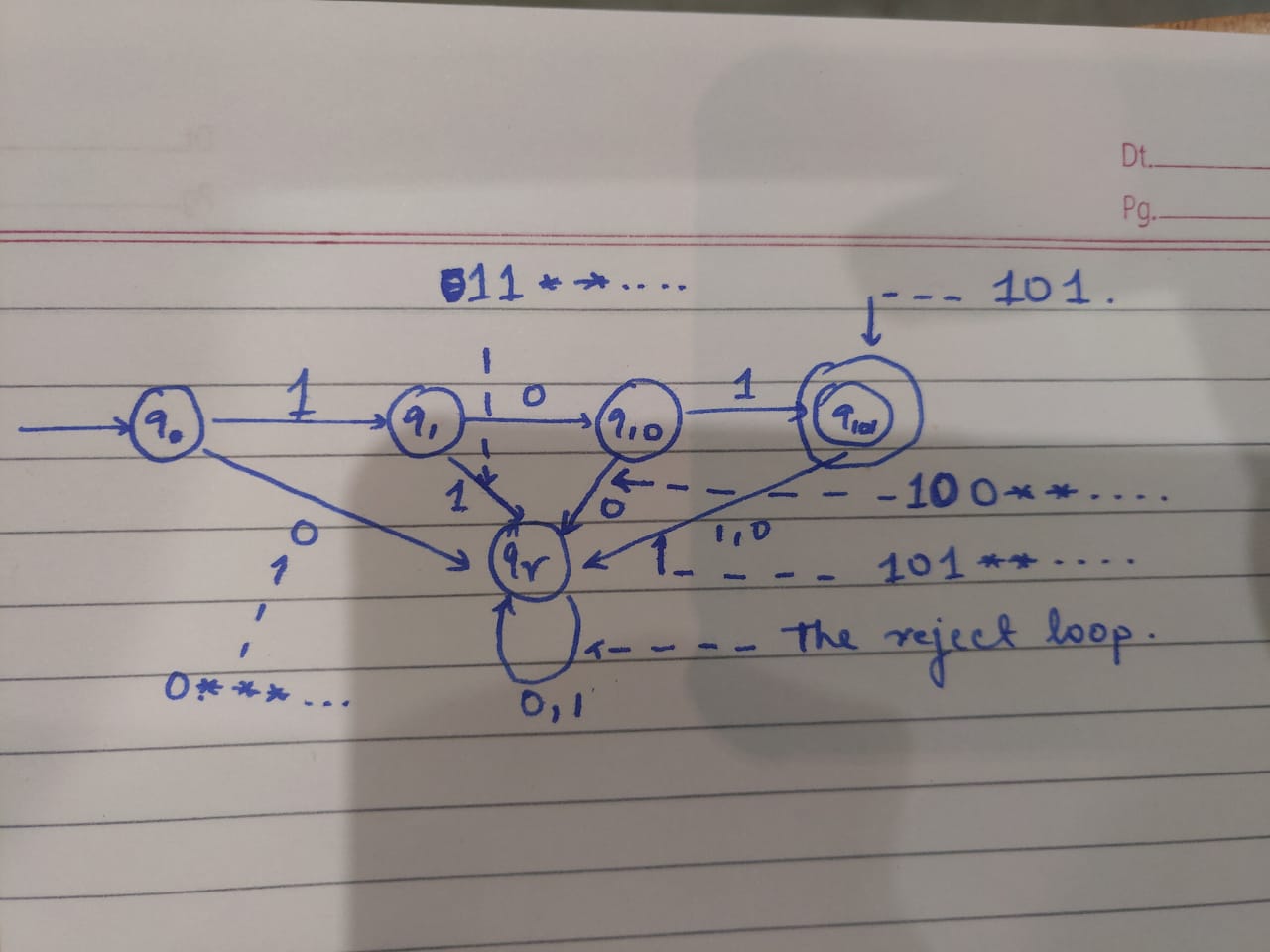
Side note
FSAs can be implemented in more than one ways. Is there a minimal implementation?
- Define a Finite State Automaton that recognizes the language L = {s | s has equal 0s and 1s}, Σ = {0,1}
r0 → r1 → … → ri → … → rn
Continued in next class…