Want to contribute? Click here to suggest edits or additions.

Finite State Automaton

M = (Q, Σ, δ, q₀, f) There is a set of states Q which M manipulates by δ over Σ and the string is accepted if it lies in f ⊂ Q, starting from q₀.

q₀ ∈ Q, f ⊂ Q

M always reads the entire input.

Accepting a string

Given a string, S = c₀,c₁…c_n, M accepts S iff ∃ r₀, r₁, … r_n+1 ∈ Q, st

1. r₀ = q₀
2. r_{i + 1} = δ(r_i, c_i)
3. r_n+1 ∈ f

A language is recognized by M, iff L = {s | M accepts s}.

Example

1. Define a Finite State Automaton that recognizes the language L = 101, Σ = {0,1}. Look at Fig 1 for implementation.

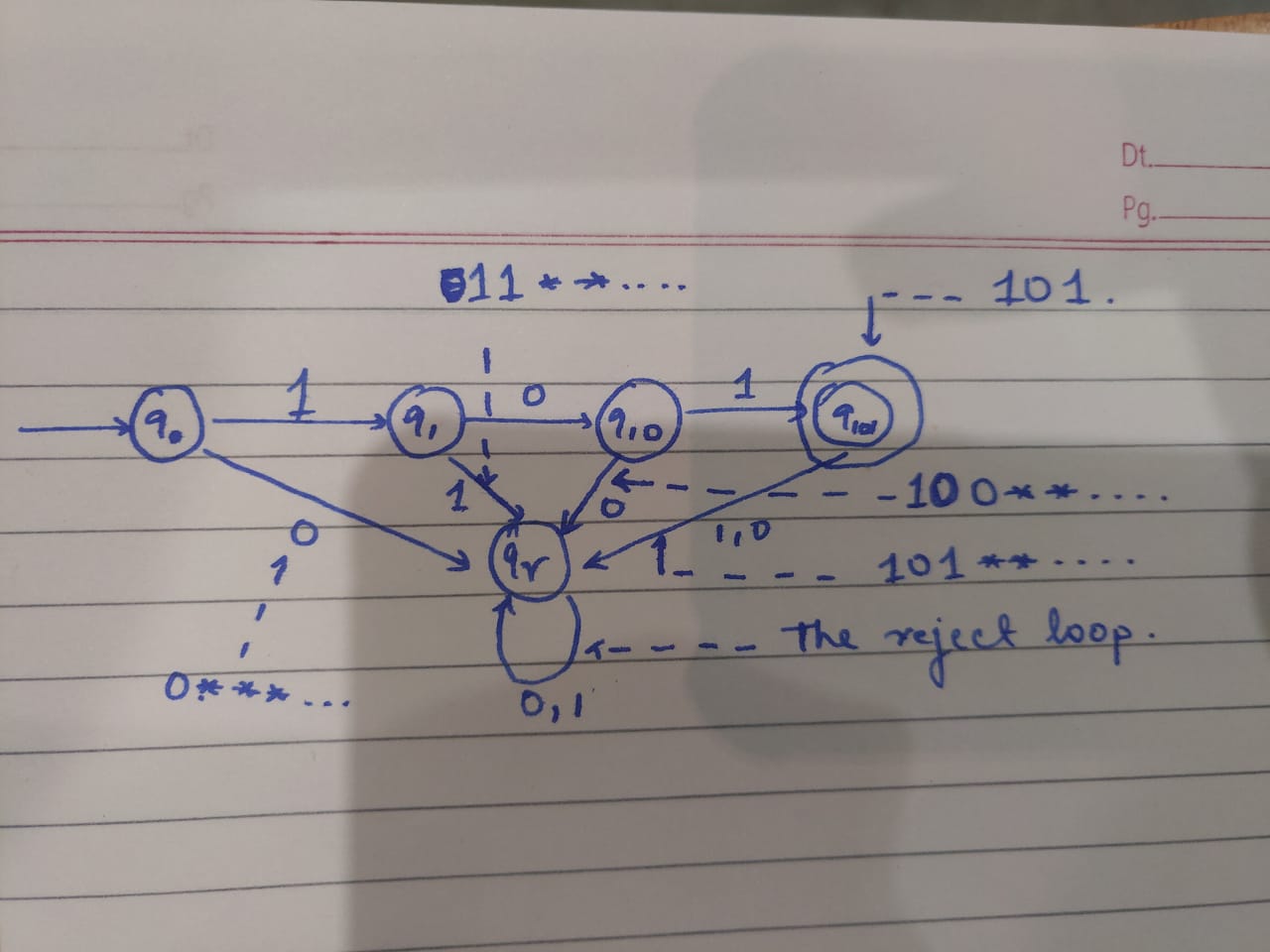
Side note

FSAs can be implemented in more than one ways. Is there a minimal implementation?

1. Define a Finite State Automaton that recognizes the language L = {s | s has equal 0s and 1s}, Σ = {0,1}

Pigeonhole Principle

r₀ → r₁ → … → r_i → … → r_n

Continued in next class…